データの分析を開始する。前回安易に選んだ分析対象は、プロットの段階で一筋縄ではいかないことが予想されたが、さてどうなる。
これから行う作業のまとめ
- WTIと1618の累積収益率の系列に単位根があるか調べる
- 線形モデルを当てはめ
- 誤差項の系列に単位根があるか調べる
検定の基本事項
これから各種の検定を行なっていくわけだが、その前に基本事項を押さえておく。
統計的仮説検定
ここで言う検定とは、統計的仮説検定のことを指す。 同時に起こることのない2つの仮説(帰無仮説と対立仮設)を立てて、 データにもとづいてどちらの仮説を受け入れるかを確率をもとに導く方法である。
二者択一の判断であり、未知の果物は何かという問いに対し2つの仮説「リンゴである」と「ミカンである」を設定することはない。 どちらの仮説も誤りで、未知の果物はバナナのというこがあり得るからだ。 そのため、「リンゴである(帰無仮説)」と「リンゴではない(対立仮説)」という互いに背反な仮説を設定するのだ。
全ての状況をカバーできる2択を用意しても、以下の2つの判断ミスが発生し得る。
- (タイプ1)帰無仮説が正しいにも関わらず、帰無仮説を却下してしまう
- (タイプ2)帰無仮説が正しくないにも関わらず、帰無仮説を採用してしまう
| 帰無仮説は正しい | 帰無仮説は誤り | |
|---|---|---|
| 帰無仮説を採用 | タイプ2のミス | |
| 帰無仮説を棄却 | タイプ1のミス |
p値
データを検定にかけるとp値が出力される。このp値はタイプ1の誤りが発生する確率を表す。 p値が十分に小さいという事は、タイプ1のミスが発生する確率が小さいことを意味し、帰無仮説を棄却して対立仮説を採用すればよいことになる。
この判断は、『帰無仮説が正しいにも関わらず、帰無仮説を却下してしまう』というミスが起こる確率が低いのだから、帰無仮説を却下しても問題ないという考えによる。
有意水準
p値がどのぐらい小さければ帰無仮説を棄却することが妥当と言えるだろうか。この水準のことを有意水準と呼ぶ。
有意水準の値としては、0.05 (= 5%) を用いるのが一般的であるが、そのとり方は学問・調査・研究対象によっても違いがあり、社会科学などでは0.1(10%)を用いる場合もあり、厳密さが求められる自然科学では0.01(1%)などを用いる場合もある。
ADF検定
基礎的な事項を押さえたところで、前回作成したデータが単位根過程かどうかを調べる作業に入ろう。
系列に単位根があるかを調べる検定を単位根検定と呼び、その1つがADF検定(augmented Dickey–Fuller test)である。 ADF検定は、帰無仮説を「単位根がある」、対立仮説を「単位根がない」として検定を行う。
この検定で出力されるp値が、0.05以下であれば、帰無仮説である「単位根がある」が棄却され、対立仮説の「単位根がない」が採用されることになる。
逆に0.05より大きなp値が出力されれば、帰無仮説が採用されて単位根があるということになり、 系列にはトレンドがあるものの差分系列には定常性の特徴を持つ系列であるとみることができる。
ADF検定を行う
それでは、前回作成した累積収益率の系列に対してADF検定を行なってみる。
pythonでは以下のツールが公開されている。
statsmodels.tsa.stattools.adfuller
from statsmodels.tsa.stattools import adfuller
ADF_wti_cr = adfuller(df['WTI_JPY_cr'])
ADF_1618_cr = adfuller(df['_1618_cr'])
print('ADF_wti_cr pvalue:', ADF_wti_cr[1])
print('ADF_1618_cr pvalue:', ADF_1618_cr[1])
ADF_wti_cr pvalue: 0.704678893131938
ADF_1618_cr pvalue: 0.838232547414905
どちらのp値も0.05以上であり、単位根過程でありそうだ。 プロットからも予想はついていたが、これで第一関門突破である。
線形モデル
続いて線形モデルの当てはめを行う。まず、1618とWTIの価格の関係を直線で表現できそうかどうかを散布図で確認してみる。
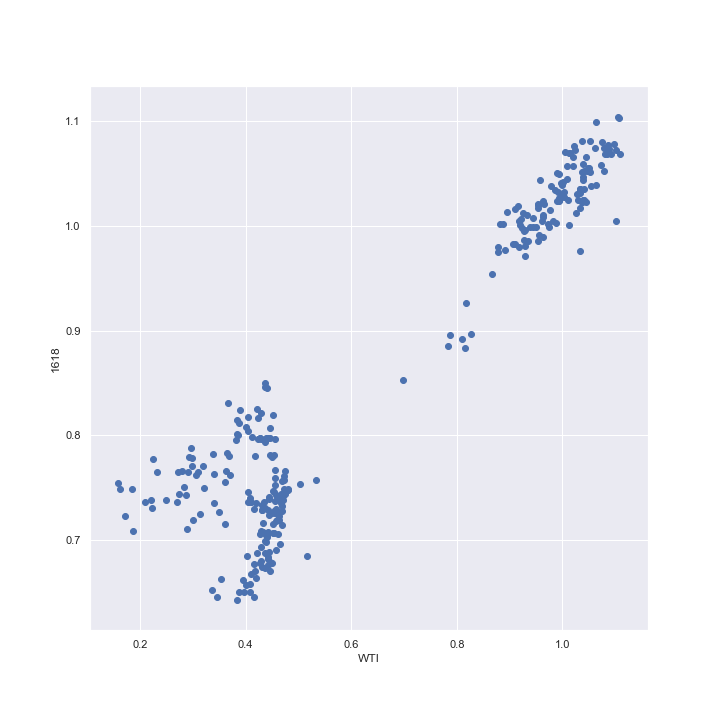 プロットは第1、第3象限に集中していることから概ね正の相関がありそうである。特に急落前はその傾向が強そうだ。
真ん中あたりにプロットが少ないのは、どちらの銘柄も急落前と急落後で異なる水準を価格が推移しており、そこにデータが集中しているためだろう。
プロットは第1、第3象限に集中していることから概ね正の相関がありそうである。特に急落前はその傾向が強そうだ。
真ん中あたりにプロットが少ないのは、どちらの銘柄も急落前と急落後で異なる水準を価格が推移しており、そこにデータが集中しているためだろう。
この散布図に2つの銘柄の関係を表現する直線を引くというのが、これからやろうとしていることだ。 を1618、をWTIとして線形モデルの当てはめる。
つまり、最も誤差が小さくなるとの推定を行うということである。
import statsmodels.api as sm
x = df['WTI_JPY_cr']
y = df['_1618_cr']
X = sm.add_constant(x.values)
model = sm.OLS(y, X)
results = model.fit()
print(results.summary())
OLS Regression Results
==============================================================================
Dep. Variable: _1618_cr R-squared: 0.893
Model: OLS Adj. R-squared: 0.892
Method: Least Squares F-statistic: 2473.
Date: Prob (F-statistic): 4.92e-146
Time: Log-Likelihood: 483.00
No. Observations: 299 AIC: -962.0
Df Residuals: 297 BIC: -954.6
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 0.5559 0.007 83.340 0.000 0.543 0.569
x1 0.4658 0.009 49.727 0.000 0.447 0.484
==============================================================================
Omnibus: 3.672 Durbin-Watson: 0.122
Prob(Omnibus): 0.159 Jarque-Bera (JB): 2.709
Skew: 0.077 Prob(JB): 0.258
Kurtosis: 2.560 Cond. No. 4.85
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
モデルの評価
OLS Regression Resultsは、「=====」の区切りで3つのパートに分かれている。
- データに関する情報と推定したモデルの特性を示す情報
- 回帰係数に関する情報
- 誤差項に関する情報
R-squared(決定係数)
説明変数が目的変数のどれくらいを説明できるかを表す値で、0~1の間の値を取る。1に近いほど説明できていることになる。
Log-Likelihood(対数尤度)
想定した回帰モデルから見て、実際に得られた標本がどの程度もっともらしいか。大きい方が良い。
AIC(赤池情報量基準)
回帰式の当てはまりの良さを示す。小さいほど良い。
coef(回帰係数)
constが、x1がのそれぞれの値。
std err(係数の標準誤差)
係数の推定値の標準誤差。小さいほど精度の高い推定。
t(t値)
係数の有意性(意味がある説明変数かどうか)を検定するための統計量。 t 値=係数の推定値/係数の標準誤差。概ね 2 より大きければ良い。
P>|t| (t検定に基づくp値)
説明変数として意味の無い(係数がゼロである)確率。小さければ意味のあ る説明変数である(「有意」である)と判断。
プロット
線形回帰を行った結果、得られたのが下のモデルである。このモデルによって予想される1618の値を先程の散布図に重ねてみる。
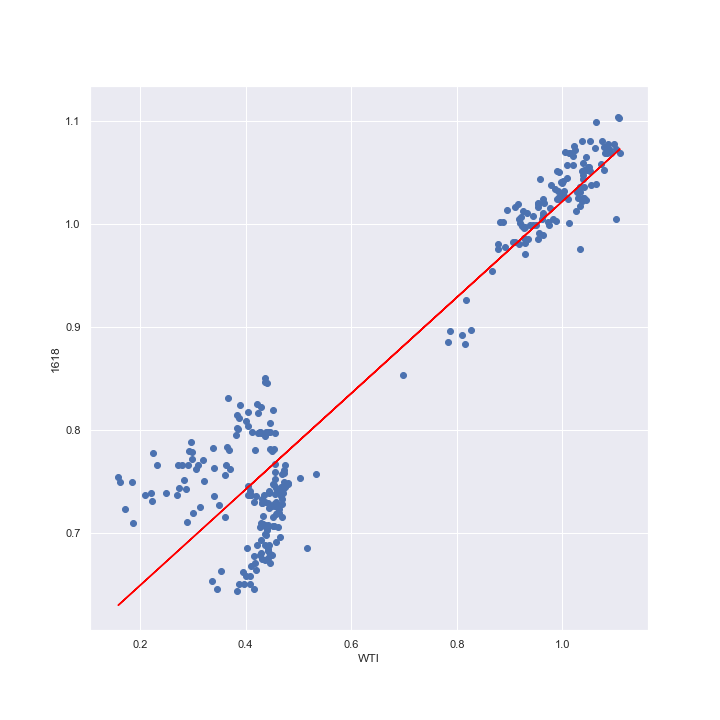 右上の暴落前のデータ群に対しては赤の線でよく説明できている。その一方で、左下の暴落後のデータに対しては微妙なところである。
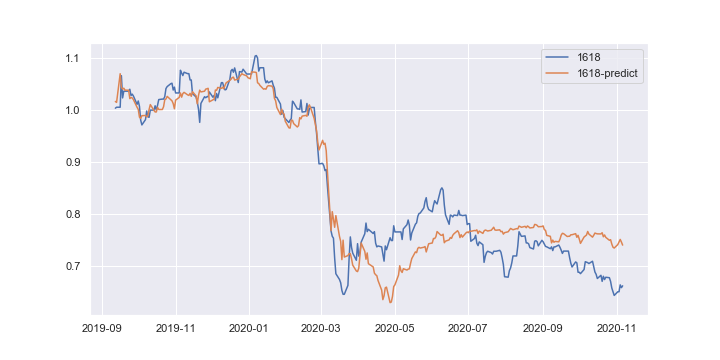
これは、1618の現実値と予想値をプロットするとより鮮明になる。
右上の暴落前のデータ群に対しては赤の線でよく説明できている。その一方で、左下の暴落後のデータに対しては微妙なところである。
これは、1618の現実値と予想値をプロットするとより鮮明になる。
参考リンク
誤差項
さて、プロットで確認したように、予測値と実際のデータの間には誤差があるわけだが、それはさしたる問題ではない。
最大の関心ごとはこの誤差の系列に定常性が見られるかである。
もし定常であれば、1618とWTIは共和分の関係にあることになり、ペアトレードへの道が開ける。
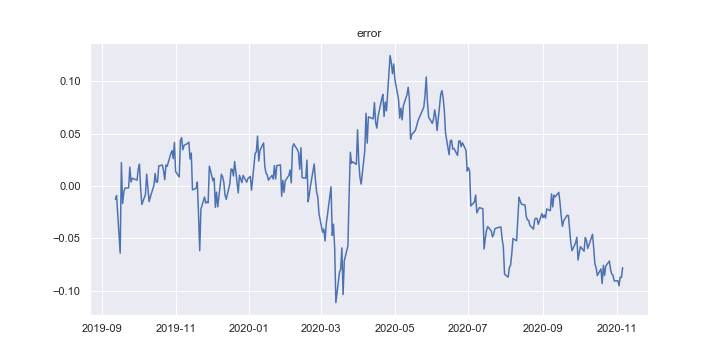
p値が0.05以下であれば、ADF検定の帰無仮説である「単位根がある」が棄却され、共和分の関係と見なすことができる。
DF_err = adfuller(df['error'])
print('ADF_error pvalue:', ADF_err[1])
ADF_error pvalue: 0.4371776884355675
0.43
続く…

