2021年10月20日
ポジションのベガ値
| ポジション | ベガ値 | |
| 原資産 | ロング | ゼロ |
| ショート | ゼロ | |
| コール | ロング | プラス値 |
| ショート | マイナス値 | |
| プット | ロング | プラス値 |
| ショート | マイナス値 | |
Volatility of Volatility
デルタとガンマが原資産価格の変動に対するプレミアムの価格変動リスクであるのに対し、ボラティリティの変動に対するプレミアムの価格変動リスクを「ベガ(vega)」と呼ぶ。
$$ vega = \frac{プレミアムの変化}{ボラティリティの変化} $$
ベガとは本来、「原資産のボラティリティの変化に対するオプション理論価格の反応度合い」を示すものだが、 トレーダーは「インプライド・ボラティリティ(IV)が1%変化した時のオプション価格の変化率」と捉える。
オプションのベガが0.15だったとする。 このオプションの理論価格がボラティリティ20%で3.25ドルだったら、ボラティリティ21%で理論価格は3.40ドル、ボラティリティ19%で理論価格は3.10ドルになる。
ベガの絶対値が大きいと、ポートフォリオの価値はボラティリティの変化に敏感に反応する。逆にベガの絶対値が小さいと、鈍感となる。
ちなみに「ベガ」はギリシア文字ではない。学術的文献ではギシリア文字で統一するために「カッパ($\kappa$)」が使われたりもする。
ボラティリティを売買する
オプションを買えば、それがコールであれプットであれ、ベガ値はプラスとなる。この時、ボラティリティが上昇すれば、プレミアムが上昇し利益となる。 ボラティリティの上昇とプレミアムの上昇はイコールである。
したがって、オプションの買いはボラティリティを買っていることに他ならない。同様に、オプションの売りは、ボラティリティの売りである。
オプション価格 = 本質的価値 + 時間価値 + ボラティリティ価値
ただし、オプション価格はボラティリティだけで決まるものではないので、ボラティリティが上昇しても、それ以上に本質的価値が下がれば、プレミアムも下がることになる。同様に、タイムディケイによる減価に負けてもプレミアムは下がる。
見方を変えれば、原資産価格に変動が無くても、オプショントレードでは利益を得るチャンスがあるということになる。
- 原資産価格変わらずでも、IVが変化してオプション価格が変動する
- 原資産価格変わらずでも、時間の経過によりオプション価格が減価する
速さ x 時間
オプションは満期の段階でITMになっていないと無価値となる。これが他の金融商品との大きな違いである。 オプションがITMというゴールに向けて走っているとすると、ゴールできるかどうかが最大の関心事である。
仮にゴールまでの距離が100㎞だとしよう。時速10㎞で走っていてゴールまでたどり着けるかどうか。これは時間がどのぐらいあるか次第である。 残り10時間でゴールまでたどり着けるか。これは速さ次第である。
ベガはスピードメーターで、セータは時計と考えると分かりやすい。
ベガの特徴
残存日数との関係
| 原資産価格 | 100 |
| ボラティリティ | 20% |
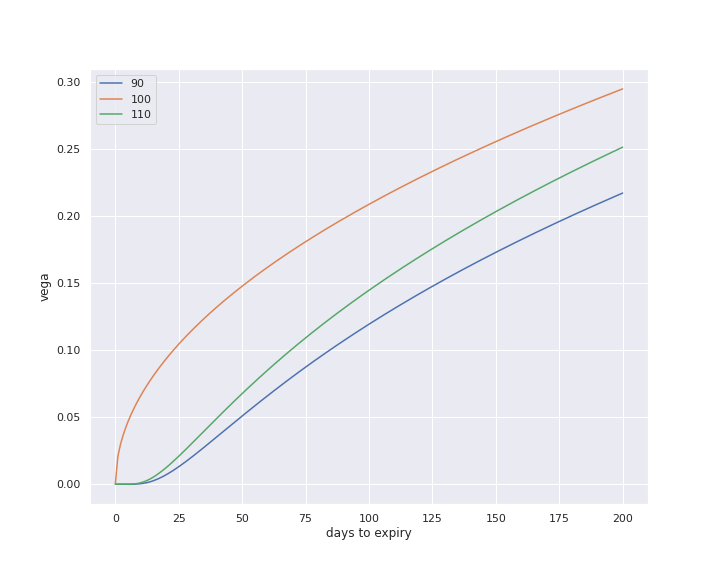
コールのベガと残存日数
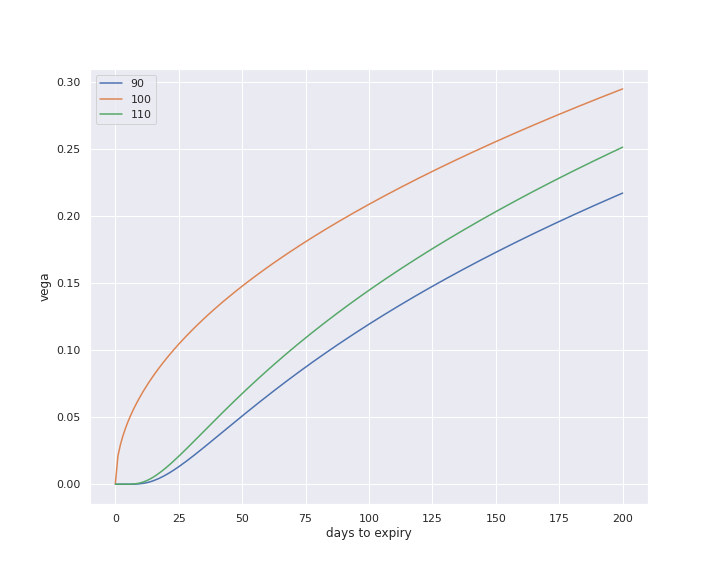
プットのベガと残存日数
原資産価格とボラティリティを固定し、残存日数を変化させる。
まず、コールとプットはまったく同じプロットとなることが確認できる。 そして、ベガ値はATMが常に最大となる。つまり、ボラティリティの変化に最も敏感なのはATMということだ。
オプション価格はITMが高くOTMが安くなる。 オプション価格が0.15値上がるとしても、そのインパクトは基となる数値が小さいほうが大きい。 したがって、オプション価格の変化率はOTMが最大となる。 この特徴は、「Put Ratio Back Spread」などを組むときに重要になるだろう。
権利行使価格の異なる3つのオプションに共通するのは、時間の経過に伴ってベガ値は減少することである。 中でもATMは残存日数が50日を過ぎた辺りから減少のスピードが増すことが見て取れる。
ボラティリティとの関係
| 原資産価格 | 100 |
| 残存日数 | 60日 |

ボラティリティとベガ
こちらは、原資産価格と残存日数を固定し、ボラティリティを変化させたものだ。
上を水平に走るのがATMのベガである。 OTMとITMのベガは、ボラティリティが低くなるとその分下がるのを確認できるが、ATMのベガは一定となっている。 つまり、ATMのベガはボラティリティ変化の影響を受けないということになる。

