HVの計算式とpythonでの実装。HVを計算する期間による違い。今後のボラティリティの予測方法。
2021年11月22日
変化の割合
変化率
「変化量をもとの値で割った値」を変化率と言います。
100から150に上昇したとすれば、
変化率は0.5です。これに100を掛けるとパーセントになり(Percentage Change)、50%の上昇と見ることができます。
では、逆に150から100に下落した場合はどうなるでしょうか。
同じ50の変化なのに、変化率は-0.333…となります。 変化率は上昇と下落で異なる値となるので少々扱いづらい面があります。
対数差分
系列を対数に変換し、その差分を取った系列を対数差分系列と言います。 対数差分は変化率と同等のものとして扱うことができます。
それは、変化分が小さいとするとき、1次のテイラー展開により以下が成立するためです。
式の一番右側は、変化率と同じ式になっていることが確認できます。 対数差分の場合、上昇も下落も符号の逆転した同じ値となります。
import numpy as np
import pandas as pd
time_series_data = pd.Series([x for x in range(10)])
log_diff_series = np.log(time_series_data).diff(1)
ヒストリカル・ボラティリティ
ボラティリティは変化率の標準偏差です。上記で確認したように、対数差分系列は変化率として扱えますので、
とすれば、
で計算できます。
でも、同じ意味です。
年換算
「」の部分は、ボラティリティは年率で表示されるのが一般的なので、形式を合わせる操作です。
ボラティリティは時間の平方根に比例するという特性を持つので、365ではなくとなります。 「」はパーセントとして見るためです。
また、365日ではなく年間の営業日数での換算も一般的です。 祝日の多い日本市場の場合240-245日、アメリカ市場の場合250-255日などが採用されます。 その年のカレンダーにより営業日数は若干異なるため、絶対的な数字はありません。
平方根が整数となる256()も多く使われているようです。 年次ボラティリティを16で割れば、近似した日次ボラティリティを簡単に求められるので、実務面でのメリットがあります。
期間(n)
式の中にある「」は標準偏差を計算する期間です。 通常、データの数が多ければ多いほど正確な結果が得られますが、ボラティリティは時間と共に変化することから、古すぎるデータを将来の予測に用いることは適切でない場合があります。
HVを計算するのは将来の予測のためだと言えます。 具体的にはオプションの理論価格を計算する際に必要なボラティリティの推定値としての利用などです。
満期まで30日のオプションの理論価格を計算するのであれば、満期日までの日数に等しい直近30日の日次リターンからボラティリティを計算し、それをインプットに採用することは筋が通っています。
ゼロ平均ボラティリティ
期間を30日とするボラティリティを計算するとして、もし30日の全ての変化率(対数差分)が1%ピッタリだったらどうなるでしょう。
当然、その平均も1%になります。その結果、上記の式で計算されるボラティリティはゼロになってしまうのです。 株価は動いているのだから、これは事実をまったく反映していません。
この問題は、
- 平均の変化率をゼロにする
- 平均の変化率を無リスク金利とする
ことで回避ができます。
変化率をゼロとした場合のボラティリティの計算式は以下のようになります。
限られたサンプルから真の分散(不変分散)を推定するためには、分母にサンプル数から1を引いたを取る必要がありますが、平均がゼロで既知であるなら分母はとなります。
期間の違いによるHVの変化
実際のデータを使い、取る期間を変えるとHVにどのような変化があるかを確認してみます。
TradingViewで「S&P500ミニ先物(当限つなぎ足)(ES1!)」の価格データをエクスポートしてみました。 2020年1月16日から2021年10月14日までの441営業日分のデータが取得できました。
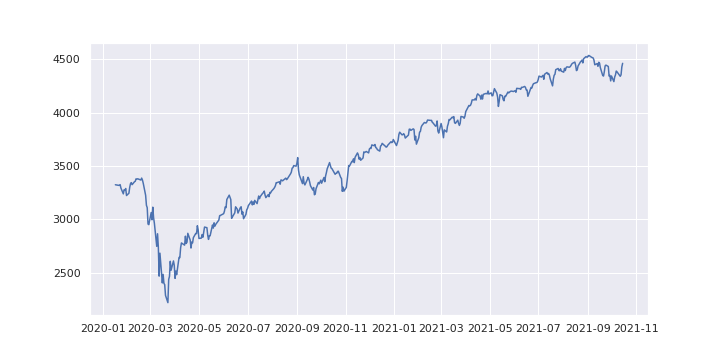
2020年の2月から3月にかけて、新型コロナウィルスの影響で急落。その後は右肩上がりの上昇を続けています。 急落から反発の局面では高いHVとなっているはずです。
対数差分系列の作成
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
FILE ="CME_MINI_DL_ES1!, 1D.csv"
df = pd.read_csv(FILE, index_col="time")
df.index = pd.to_datetime(df.index, unit='s')
df['log_diff'] = np.log(df.close).diff(1)
df.drop(['open','high','low'], axis=1, inplace=True)
df.head()
df.head()の出力
| time | close | log_diff |
| 2020-01-16 23:00:00 | 3325.00 | NaN |
| 2020-01-20 23:00:00 | 3319.50 | -0.001656 |
| 2020-01-21 23:00:00 | 3319.75 | 0.000075 |
| 2020-01-22 23:00:00 | 3326.00 | 0.001881 |
| 2020-01-23 23:00:00 | 3293.50 | -0.009820 |
HVの計算
ヒストリカル・ボラティリティを算出する期間を変えていくつか計算してみます。 ここでは10日、30日、50日の3パターンを計算します。
periods = [10, 30, 50]
for i in periods:
df[f'HV_{i}'] = df['log_diff'].rolling(i).std() * 100 * np.sqrt(256)
df[['HV_10', 'HV_30', 'HV_50']].tail()
df.tail()の出力
| time | HV_10 | HV_30 | HV_50 |
| 2021-10-10 22:00:00 | 17.122113 | 12.998005 | 11.520254 |
| 2021-10-11 22:00:00 | 13.650072 | 12.893195 | 11.521547 |
| 2021-10-12 22:00:00 | 13.739062 | 12.964967 | 11.394647 |
| 2021-10-13 22:00:00 | 14.236314 | 13.999718 | 11.987436 |
| 2021-10-14 22:00:00 | 13.843118 | 14.164805 | 12.029762 |
プロット
違いを確認するために3つの期間のHVを一緒にプロットしてみます。
plt.figure(figsize=(10, 5))
for i in periods:
plt.plot(df.index, df[f"HV_{i}"], label=i)
plt.legend()
plt.show()
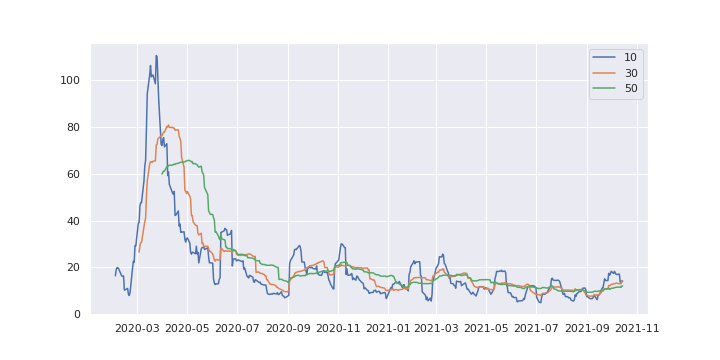
どの期間設定でも急落から反発の局面では高いHVとなっています。ただし、期間設定により記録した最大のHVに大きな差があります。 また、移動平均線の期間設定のように、短いと反応が早く、長いと反応が遅くなるのが見て取れます。
最も短い10日は反応は速いものの変動が激しすぎて、傾向を掴むのには適していないように見えます。 この中で最も長い50日は反応が遅く、ボラティリティが落ち着いた局面では水平に近くなってしまっています。
プロットする期間を相場が落ち着きだした2020年9月以降に絞ってみます。

このぐらいのスケールであれば、50日でも十分に傾向が掴めそうです。
HVの予測
一般的なチャートの分析では、長期と短期の移動平均線のクロスで相場の転換を掴んだりします。 それと同じような分析がHVでも可能なように見えるのは興味深いです。 短期HVが長期HVをクロスして越えると、その後しばらくはボラティリティの上昇傾向が続くといった具合です。
30日(オレンジ)では、高値を切り下げて下落トレンド入りするというのが2か所ほど見えます。 期間設定によってはZIGZAGの分析も機能するかもしれません。
ゼロ平均ボラティリティとの比較
通常のボラティリティの計算結果と、ゼロ平均ボラティリティの計算結果の差を確認しておきます。
df['HV_30'] = df['log_diff'].rolling(30).std() * np.sqrt(256) * 100
df['HV_30_zero'] = np.sqrt(256 / 30 * (df['log_diff']**2).rolling(30).sum())* 100
df[['HV_30', 'HV_30_zero']].tail()
df.tail()の出力
| time | HV_30 | HV_30_zero |
| 2021-10-10 22:00:00 | 12.998005 | 12.914323 |
| 2021-10-11 22:00:00 | 12.893195 | 12.869416 |
| 2021-10-12 22:00:00 | 12.964967 | 12.901333 |
| 2021-10-13 22:00:00 | 13.999718 | 13.808252 |
| 2021-10-14 22:00:00 | 14.164805 | 13.953404 |
計算式をコード化する部分にちょっと不安がありますが、似たような計算結果になりました。
日々の値動きはしっかり反映されているようですが、ゼロ平均ボラティリティの計算結果の方が全体的に小さな値となっています。

