2021年10月9日
損益図は満期での本質的価値
カレンダー・スプレッドは、コールもしくはプットを「同一権利行使価格、異なる満期」で組むスプレッドです。 「ホライゾンタル(水平、英: holizontal)スプレッド」の基本形となります。 タイム・スプレッドとも呼ばれるのは、タイムディケイとIVの上昇から利益を得ようとするためです。
カレンダー・スプレッドが採用されるのは、主にトレーダーが短期と長期で異なる予測を立てる場合です。 例えば、短期的には緩やかな値動きを見込み、長期的にはそこそこ動くことを見込むといったケースがこれにあたるでしょう。
ボラティリティの見込みが「中立」であっても、セータ狙いでカレンダー・スプレッドを採用することはあります。
同一満期で組まれる「バーティカル(垂直、英: vertical)スプレッド」の損益図は、満期日における各オプションの本質的価値(Intrinsic Value)の合計を原資産の価格ごとにプロットしたものです。
カレンダー・スプレッドの場合、少なくとも2つの満期日が存在しています。 期近のオプションの満期日で損益図を描こうとするなら、期先のオプションを反映することは出来ません。 残存期間のあるオプションでは本質的価値だけではなく付帯的価値(Extrinsic Value)が重要になるためです。
カレンダー・スプレッド(以下、Calendar Callを想定)の最大利益は、ショートした期近のオプションがATMで満期を迎え(権利行使しても意味がない)、ロングした期先のオプションのIVが上昇した時に得られます。
しかし、具体的な額を計算することができません。これは損益分岐点も同様です。 最大損失額はポジション時の支払いプレミアム(initial net debit)となります。
無理やりにでもカレンダー・スプレッドの損益図を描くため、期近のオプションの満期日に照準を合わせます。 期近のオプションの本質的価値は簡単に計算できます。後は期近の満期時点での期先のオプションをどう評価するかです。
カレンダー・スプレッドの損益図
期先のオプション価格は計算できないので、「見積もる(guesstimate)」ことになります。 ブラック・ショールズ・モデルを使い、期先のオプション価格を見積もります。
この計算にはpy_vollibというライブラリを使いたいと思います。オプション価格、IV、グリークを計算してくれるライブラリです。
➡ 公式ドキュメント
前提
道中のIVと金利は変動しないことを前提とします。 IVの変動は損益に大きな影響を与えるので、期近満期時点の損益もIVの変動次第で大きく変わることになります。
ライブラリのインポート
何はさておき、ライブラリのインポートです。
# Data manipulation
import numpy as np
import pandas as pd
# To plot
import matplotlib.pyplot as plt
import seaborn as sns
# BS Model
from py_vollib.black_scholes import black_scholes as bs
from py_vollib.black_scholes.implied_volatility import implied_volatility as iv
py_vollibには3つのモデルが含まれます。
- Black
- Black-Scholes
- Black-Scholes-Merton
今回は「Black-Scholes」を採用し、オプション価格を計算するblack_scholesと、IVを計算するimplied_volatilityの2つモジュールをインポートしておきます。
「Black-Scholes-Merton」は、配当落ちを考慮してマートンがBSモデルも改良したものです。 1989年に大阪証券取引所が日経225のオプションを開設し、その時に採用されたのはこのモデルだったそうです。
カレンダー・スプレッドの作成
実際の価格データを基にカレンダー・スプレッドを組んでみたいと思います。 対象とするのは「SPDR S&P 500 ETF Trust (SPY)」 (Yahoo! finance)です。
2021年10月9日現在の価格は437.86となっていました。 権利行使価格を438.00とし、10月15日満期と11月19日満期のコールでカレンダー・スプレッドを組みます。
コールの価格
| 満期 | 権利行使価格 | オプション価格 | 残り日数 |
| 2021年10月15日 | 438.00 | 3.26 | 7日 |
| 2021年11月19日 | 438.00 | 9.19 | 41日 |
# Price data
SPY_price = 437.86
strike_price = 438.00
oct_call_price = 3.26
nov_call_price = 9.19
setup_cost = nov_call_price - oct_call_price
# Days to expiry
days_to_expiry_oct_call = 7
days_to_expiry_nov_call = 41
# Range of values for Nifty
sT = np.arange(0.8*SPY_price, 1.2*SPY_price, 0.5)
# interest rate for input to Black-Scholes model
interest_rate = 0.0
IVの計算する
続いて、それぞれのオプションのIVを計算します。
# Front-month IV
oct_call_iv = iv(price=oct_call_price,
S=SPY_price,
K=strike_price,
t=days_to_expiry_oct_call / 365,
r=interest_rate,
flag='c')
print("Front Month IV {:.2%}".format(oct_call_iv))
# Back-month IV
nov_call_iv = iv(price=nov_call_price,
S=SPY_price,
K=strike_price,
t=days_to_expiry_nov_call / 365,
r=interest_rate,
flag='c')
print("Back Month IV {:.2%}".format(nov_call_iv))
コールの価格
| 期近 | 13.76% |
| 期先 | 15.82% |
期近の満期時点でのコール価格を計算する
# Changing days to expiry to a day before the front-month expiry
days_to_expiry_oct_call = 0.001
days_to_expiry_nov_call = 41 - 7
df = pd.DataFrame()
df['SPY_price'] = np.arange(0.9*SPY_price, 1.1*SPY_price, 1)
df['oct_call_price'] = np.nan
df['nov_call_price'] = np.nan
# Calculating call price for different possible values of SPY
for i in range(0, len(df)):
df.loc[i, 'oct_call_price'] = bs(S=df.iloc[i]['SPY_price'],
K=strike_price,
sigma=oct_call_iv,
t=days_to_expiry_oct_call / 365,
r=interest_rate,
flag='c')
df.loc[i, 'nov_call_price'] = bs(S=df.iloc[i]['SPY_price']+1,
K=strike_price,
sigma=nov_call_iv,
t=days_to_expiry_nov_call / 365,
r=interest_rate,
flag='c')
期近のコールもBSモデルで計算するために、残存日を0.001にしました。SPYの価格が取り得る範囲を現在価格の上下10%として、1ドル刻みでつくった原資産価格系列ごとにコールの価格を計算していきます。
期先のオプション価格の計算において原資産価格に+1しているのは、年間で3%ほどの上昇をしていると仮定してのもの。 これによりよく見かけるカレンダー・スプレッドの損益図と同じような形状となります。 +1をしなかった場合のプロットは左右対称に近くなります。
損益図
df['payoff'] = df.nov_call_price - df.oct_call_price - setup_cost
sns.set()
plt.figure(figsize=(10, 5))
plt.plot(df.SPY_price, df.payoff)
plt.vlines(strike_price, ymin =-6, ymax=4, colors='white', linestyle='dashed', linewidth=2)
plt.show()
カレンダー・スプレッドの損益図
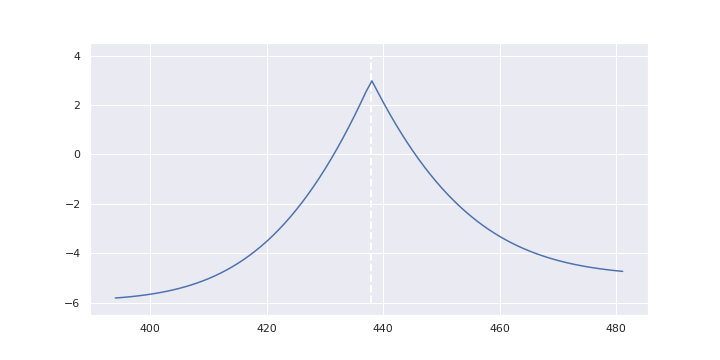
権利行使価格と同じ価格で最大利益となり、上昇しても下降しても損益は悪化します。 繰り返しますが、これはIVに変化が無かったと仮定してのものです。
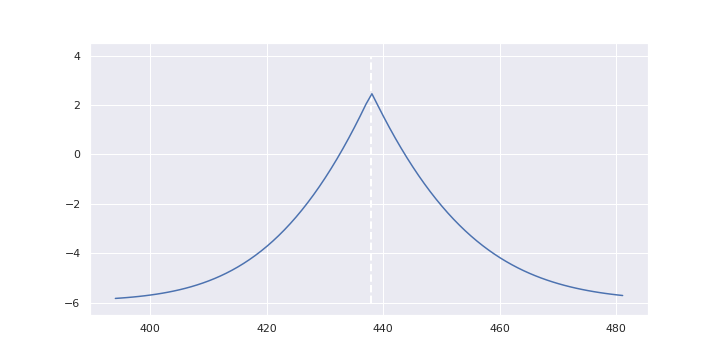
+1しなかった場合の損益図