サイクルの理解を深めるための基礎知識
2022年6月25日
信号とシステム
信号
数学には関数「$f(x)$」という概念がある。これを工学では信号「$f(t)$」と呼ぶ。 「$t$」は時間を表す。
| 時間(x軸) \ 振幅(y軸) | 連続 | 離散 |
| 連続 | アナログ | 多値 |
| 離散 | サンプル値 | ディジタル |
横軸(t軸)を飛び飛びにする作業を離散化と言い、縦軸(y軸)を飛び飛びにする作業を量子化と言う。 こうした操作を行った信号をディジタル信号と呼ぶ。
フーリエ解析
フーリエ級数(周期信号)
- $\sin$
- $\cos$
- $e$ (複素フーリエ級数)
フーリエ変換(非周期関数)
我々が生きている現実世界は時間領域$f(t)$である。 これを仮想世界の周波数領域(frequency domain)に変換するのがフーリエ変換。
ラプラス変換(Laplace Transform)
時間の世界から複素数の世界へ。$F(s)$は複素関数。
Z変換
Z変換はラプラス変換のディジタル版。「$k$」はディジタル(離散時間)を表す。
離散時間フーリエ変換
➡ FFT(Fast Fourier Transform)
基本的な連続時間信号
正弦波
A:最大振幅
$\omega$:角周波数 $= 2 \pi f$
$\phi$:位相(phase)
$f$は周波数(Hz)を表し、1秒間に同じことを何回繰り返すかを意味する。 回数ではなく、1秒間に「何rad」かを考えるのが角周波数となる。
1回が1周、つまり「1回 = $2\pi$」に相当するので、周波数(Hz)を$2\pi$倍したものが角周波数$\omega$となる。
正弦波は周期信号 ➡ フーリエ級数
周期性
- この時、信号$x(t)$は周期$T$の周期信号と言う
- $T$の中で、最も小さい整数$T_0$を基本周期と呼ぶ
$x(t) = \sin t$
基本周期 $T_0 = 2 \pi$
基本角周波数 $\omega_0 = 2 \pi f_0 = 2 \pi \frac{1}{T_0} = 1 rad/s$
インパルス信号(デルタ関数)
- 時刻0以外でゼロ、時刻0で無限の高さを持つ
- 面積を積分すると1
- 超関数
$$ \int _{-\infty}^{\infty} x(t) \delta (t-a) = x(a)$$
単位ステップ信号
- 負の時刻では0
- 時刻0からは1
- 微分すると単位インパルス信号
複素指数信号
- cとaは複素数
- 時間の世界の信号なのに複素数が係数
cとaが実数
- $a < 0$の時、指数的に減衰する
- $a > 0$の時、指数的に発散する
aが順虚数のとき(c=1とする)
$x(t) = e^{j \omega _0 t}$
➡ オイラーの公式
オイラーの公式
- $ \cos \omega _0 t $は偶関数
- $ j \sin \omega _0t $は奇関数
三角関数と基本周期
➡ 慶應大学講義 物理情報数学C 第二回 三角関数と基本周期
三角関数
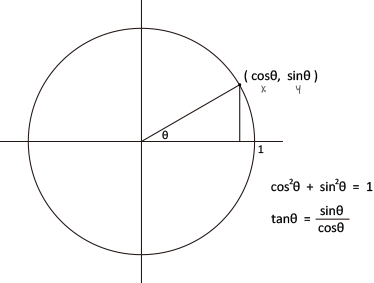
加法定理
$$ \tan (\alpha + \beta) = \frac{\sin (\alpha + \beta)}{\cos (\alpha + \beta)} = \frac{\sin \alpha \cos \beta + \cos \alpha \sin \beta}{\cos \alpha \cos \beta + \sin \alpha \sin \beta} $$
$$ = \frac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta } $$
三角関数の合成定理
$$ a \cos \theta + b \sin \theta = \sqrt{a^2 + b^2} \cos (\theta + \arctan (- \frac{b}{a}) )$$
$$ = \sqrt{a^2 + b^2} ( \frac{a}{\sqrt{a^2 + b^2}} \cos \theta + \frac{b}{\sqrt{a^2 + b^2}} \sin \theta )$$
$$ = \sqrt{a^2 + b^2} (\cos \phi \cos \theta + \sin \phi \sin \theta)$$
ただし、$\tan \phi = \frac{b}{a} \rarr \phi = \arctan \frac{b}{a}$
※加法定理
$$ = \sqrt{a^2 + b^2} \cos (\theta - \phi)$$
周期について
$$ a \cos \textcolor{red}{\omega t} + b \sin \textcolor{red}{\omega t} = \sqrt{a^2 + b^2} \cos (\textcolor{red}{\omega t} - \arctan \frac{b}{a}) $$
同じ周期の$\sin$もしくは$\cos$を足し合わせても、同じ周期が現れる。
異なる周期を合成する
$f(t) = \cos \frac{t}{3} + \cos \frac{t}{4}$の周期は?
求めたい周期を「T」とする。
$$\cos \frac{t}{3} + \cos \frac{t}{4} = \cos \frac{t+T}{3} + \cos \frac{t+T}{4} $$
が成り立つならば、周期と言える。
いま、$\cos (t + 2\pi m) = \cos t$、$^{\forall}t$:整数なので、($2\pi$ずらしたら元に戻る)
$\frac{T}{3} = 2\pi m$、$\frac{T}{4} = 2\pi n$とおくと、
$T = 6\pi m = 8 \pi n $
$m=4$、$n=3$とおくと、$T=24\pi$
一般に、信号$ f(t) = \cos \omega _1 t + \omega _2 t $が周期Tの周期信号であるためには、
$$ \frac{\omega _2}{\omega _1} = \frac{m}{n} $$が有理数でなければならない。
信号の分解
- 偶信号(even):$f(-t) = f(t)$
- 奇信号(odd) : $f(-t) = -f(t)$
偶関数はx軸対象、奇関数は原点対象。
どんな関数でも偶関数と奇関数の和で書ける(偶奇分解)
$$ x(t) = x_e(t) + x_o(t) $$ただし、
$$ x_e(t) = \frac{1}{2} (x(t) + x(-t)) $$ $$ x_o(t) = \frac{1}{2} (x(t) - x(-t)) $$$x(t) \rarr x(-t)$は、時間の反転。
テイラー展開
$t=0$の近傍で(マクロリーン展開)
$$ \sin t = t - \frac{t^3}{3!} + \frac{t^5}{5!} - \cdots$$ $$ \cos t = 1 - \frac{t^2}{2!} + \frac{t^4}{4!} - \cdots$$
$\sin$は奇関数、$\cos$は偶関数。 $\exp$は$\sin$と$\cos$の和なので、テイラー級数展開すると偶関数成分と奇関数成分が出てくる。
- 複雑なものをシンプルに
- 曲がりくねったものを微分を使って表現
- 非線形(non-linear)を線形化(1次近似)
線形時不変システム(Linear Time-Invariant System)
➡ 慶應大学講義 物理情報数学C 信号の表現,重ね合わせの理とたたみこみ積分
単位インパルス信号による連続時間信号の表現
$$ \hat{x}(t) = \displaystyle\sum_{k=-\infty}^\infty x(k\Delta) \delta _\Delta (t-k \Delta) \Delta $$
デルタ関数を使って、連続時間信号を表現できる。
インパルス応答
LTIシステムにデルタ関数を入力して、出力されるのがインパルス応答。
任意の入力$x(t)$を分割してLTIシステムに入力すると、それぞれの応答が得られる。 それらを足し合わせ(重ね合わせの理)、$\Delta \rarr 0$ の極限を計算すると、 $x(t)$に対する応答が得られるのではないか。
たたみ込み積分(Convolution)
➡ 慶應大学講義 物理情報数学C 第四回 たたみこみ積分の計算法,内積と直交
$x$:入力
$g$:インパルス応答
インパルス応答が既知であれば、どんな入力でも上記の積分を計算することで出力が分かる。 これは線形だから重ね合わせの理が成り立つため。
性質
| ① | 交換則 | $ x(t) \ast g(t) = g(t) \ast x(t)$ |
| ② | 結合則 | $ x(t) \ast \{ g_1(t) \ast g_2(t) \} = \{ x_1(t) \ast g_1(t) \} \ast g_2(t) $ |
| ③ | 分配 | $ x(t) \ast \{ g_1(t) \ast g_2(t) \} = x(t) \ast g_1(t) + x(t) \ast g_2(t) $ |
フーリエ解析
内積と直交
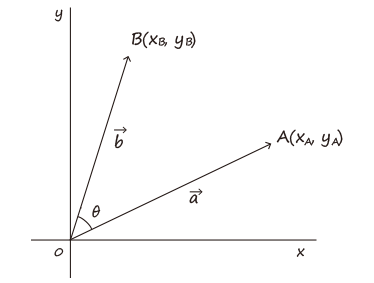
内積(inner product)
ベクトルは「大きさ」と「向き」を持つものなので、向きの異なるベクトル同士を純粋にかけ算できない。 そこで、三角比$\cos\theta$ を用いてベクトルの向きをそろえ、内積として定義する。
ベクトルの大きさ
自分自身との内積を取ると、$\theta$はゼロなので、$\cos \theta=1$となる。 したがって、大きさの2乗となる。
直交
$\vec{a} \cdot \vec{b} = 0$の時、ベクトルabは直交している。
単位ベクトル(unit vector)
$\vec{e}_x = [1, 0]$
$\vec{e}_y = [0, 1]$
平面上の任意の点は、$ \alpha \vec{e}_x + \beta \vec{e}_y$ と書くことができる。
フーリエ級数展開は、$ \vec{e}_x $と$ \vec{e}_y$が、$\sin$、$\cos$ に置き換わったもの。 正規直交関数系と呼ばれる。
信号の内積と直交
【定義1】2つの信号の内積
周期$T$の周期信号$f(t)$と$g(t)$ $$ \lt f, g \gt = \frac{2}{T} \displaystyle\int_{- \frac{T}{2}}^{\frac{T}{2}} f(t) g(t) dt $$
【定義2】信号の大きさ(ノルム)
$$ \lVert f \rVert = \sqrt{\lt f, f \gt} = \sqrt{\frac{2}{T} \displaystyle\int_{- \frac{T}{2}}^{\frac{T}{2}} f^2 (t) dt } $$
【定義3】信号の直交性
2つの信号の内積が0の時、直交しているという。 $$ \lt f, g \gt = 0 $$
例題:$f(t) = \sin \omega _0 t$, $g(t) = \sin 2 \omega _0 t$のとき、内積を計算せよ
$\lt f, g \gt = \frac{2}{T} \displaystyle\int_{- \frac{T}{2}}^{\frac{T}{2}} \sin \omega _0 t \sin 2 \omega _0 t dt $
$T= \frac{2 \pi}{\omega _0}$なので、$\frac{T}{2} = \frac{\pi}{\omega _0}$
$ = \frac{2}{T} [\displaystyle \int_{- \frac{\pi}{\omega _0}}^{\frac{\pi}{\omega _0}} \cos \omega _0 t - \displaystyle \int _{ - \frac{\pi}{\omega _0}}^{\frac{\pi}{\omega _0}} \cos 3 \omega _0 t dt ] $
$ = 0$
フーリエ級数
フランスの数学者フーリエ(1768~1830:ナポレオンの時代)は、1807年に「任意の関数は三角関数によって級数展開できる」というフーリエ級数の概念を提唱した。
フーリエ解析
級数展開
テイラー級数展開、マクロリーン級数展開など:微分が必要なので、不連続関数には適用できない。
フーリエ級数展開は周期関数に対するものであるが、微分可能性を必要としないので、不連続関数にも適用できる。
フーリエ級数展開
フーリエ級数展開は、関数を偶関数成分と奇関数成分に分解したもの。
- 無限級数展開
- どのようにしてフーリエ係数($a_n, b_n$)を決定するか ➡ 内積計算
ポイント
- 周期$T$の周期関数$f(t)$は、次式のようにフーリエ級数展開できる
$$ f(t) = \frac{a_0}{2} + \displaystyle \sum_{n=1}^{\infin} (a_n \cos n \omega _0 t + b_n \sin n \omega _0 t)$$
- 基本角周波数
$$ \omega _0 = \frac{2\pi}{T} $$
- フーリエ係数($a_n, b_n$)は、内積計算により得られる
$$ a_n = \lt f , \cos n \omega _0 t \gt = \frac{2}{T} \displaystyle\int _{- \frac{T}{2}}^{\frac{T}{2}} f(t) \cos n \omega _0 t dt $$
$$ b_n = \lt f , \sin n \omega _0 t \gt = \frac{2}{T} \displaystyle\int _{- \frac{T}{2}}^{\frac{T}{2}} f(t) \sin n \omega _0 t dt $$
- 三角関数の合成定理を用いる
$$ f(t) = \displaystyle\sum _{n=0}^{x} K_n \cos (n \omega _0 t - \theta _n)$$
ただし、
$ K_n = \frac{a_0}{2}$、$n=0$のとき ➡ 直流成分(DC成分)
$ K_n = \sqrt{a_n^2 + b_n^2}$、$n=1,2,\dots$のとき ➡ 高調波振幅
$ \theta _n = 0$、$n=0$のとき
$ \theta _n = \arctan \frac{b_n}{a_n}$、$n=1,2,\dots$のとき ➡ 位相角
関数(信号)を基本波と高調波に分解することを調和解析(harmonic analysis)と言う。
$T=2\pi$の場合のフーリエ級数
$T=2\pi$のとき、$\omega _0 = 1[rad/s]$
$$ f(t) = \frac{a_0}{2} + a_1 \cos t + a_2 \cos 2t + \cdots + b_1 \sin t + b_2 \sin 2t + \cdots $$
$$ = \frac{a_0}{2} + \displaystyle\sum _{n=0}^{x} (a_n \cos nt + b_n \sin nt) $$
ただし、
$ a_n = \lt f , \cos nt \gt = \frac{1}{\pi} \displaystyle \int_{- \pi}^{\pi} f(t) \cos nt dt $
$ ab_n = \lt f , \sin nt \gt = \frac{1}{\pi} \displaystyle \int_{- \pi}^{\pi} f(t) \sin nt dt $
フーリエ余弦級数(偶関数のとき)
$$ f(t) = \frac{a_0}{2} + \displaystyle\sum _{n=1}^{\infin} a_n \cos n \omega _0 t $$
ただし、
$ a_n = \frac{4}{T} \displaystyle \int_{0}^{\frac{T}{2}} f(t) \cos n \omega _0 t dt $
フーリエ正弦級数(奇関数のとき)
$$ f(t) = \displaystyle\sum _{n=1}^{\infin} b_n \sin n \omega _0 t $$
ただし、
$ b_n = \frac{4}{T} \displaystyle \int_{0}^{\frac{T}{2}} f(t) \sin n \omega _0 t dt $

