サイクル・インジケーターの土台となる考え。
2022年2月18日
トレードとデジタル信号処理
各種サイクル・インジケーターは、主に工学分野で活躍する「デジタル信号処理(Digital Signal Processing : DSP)」の考えをトレードに応用したものです。
チャート分析で使われるインジケーターが抱える問題の1つは、パラメーターの設定にあります。 分かりやすいところで言えば、移動平均線やRSI、ストキャスティックなどでお馴染みの「期間設定(period)」がこれにあたります。
期間設定に絶対の数値はありません。 だから、そのインジケーターが機能する時もあれば機能しない時もあるのが普通なのです。 これを解決するには、常に変化する相場に合わせて期間設定を変更し続けることが必要になります。
となると、現在の相場においてインジケーターに設定すべき期間を知る術が求められるわけですが、これは中々に難しい問題で一筋縄にはいきません。 結果論で後から「期間設定を〇〇にしたインジケーターが機能した」というのなら、いくらでも可能なのですが….
新たなアプローチ
今から20年以上前、アメリカの著名なトレーダーでもあるJohn F. Ehlers博士は、このような着想を得ました。 そして、これまでのインジケーターの弱点を克服した数々のインジケーターを発表します。
当たり前の話ですが、大元となるデジタル信号処理の理解無くして、他分野への応用は不可能です。 だから、大元の理解に挑戦しようと思ったことは何度もあるのですが、門外漢である私にとっては厳しいものでした。
それでもこれまで問題は無かったのです。 なぜなら、博士は相場に即適用できるコードの形でインジケーターを公開してくれていたからです。 計算はブラックボックスでも、使用に習熟していれば、その恩恵に預かれました。
そんなわけで理論的なところは長年放置していたわけですが、少し深いところにまで踏み込んでみようというのが今回の企画になります。
サイクル成分、トレンド成分
日々観察される値動きは、サイクル成分とトレンド成分によって形作られていると仮定します。 サイクル成分は周期的な上下運動を繰り返そうとする力、トレンド成分は一方向への継続的な動きを作り出そうとする力です。
トレンドはどこまで続くか分かりません。 一方、サイクルには周期性があるので、その特性が分かれば、その後の動きもある程度は予測できるはずです。
もし、価格変動からサイクル成分を取り除くことができれば、残るはトレンド成分によって形成された値動き、つまりトレンドになります。
トレンドを確認したら、調整を待ってトレンド再開の動きを狙うのが定跡です。 問題となるのはトレンド再開のタイミングですが、これはトレンドの方向性とサイクルの方向性が合致した時が有力になります。
ポジションを持ったら持ったで、今度はどこまで引っ張るかが悩みの種となります。 サイクルの反転により、サイクルの向きとトレンド方向との不一致が発生したとなれば、それは撤退のシグナルとして使えそうです。
このように、サイクルは、
に繋がるものなので、その理解はトレーダーにとって、大きな恩恵があるはずです。
では、サイクルを理解するとは、具体的に何か分かれば良いのでしょうか。 皆目見当が付きませんので、回り道をしながら(基礎知識を補強しながら)、サイクルについて考えて行きたいと思います。
信号
価格を「信号(情報を含む物理量)」とすれば、チャートは横軸に時間をとって信号の時間変化を記録したものだと言えます。
信号は、その性質から3つに大きく分けられます。
| 数式で表せる | 連続性 | |
| 周期信号 | 〇 | 〇 |
| 過渡信号 | 〇 | X |
| 不規則信号 | X | 〇 |
物理信号は、一般にこの3つが合成された信号です。 価格も、周期性があり、材料による一時的な動きもあり、ランダムな動きもありますから、信号として見るのにおかしな点はありません。
周期信号
価格変動は周期信号だけで完璧に説明できるほど単純なものではありません。 よく言われるのは「テクニカルは材料に対し無力だ」ということですが、だからといってテクニカル分析が必要ないとはなりません。
例え完璧じゃなかったとしても、周期(サイクル)に注目するのは意味があることだと考えます。 要は使い方、付き合い方なのです。
周期信号の最も基本的なものは正弦波信号です。これを数式で表すと以下となります。
$$ x(t) = A \sin (\omega t + \theta) $$
| A | 振幅 | 信号の大きさ |
| $\omega$ | 角周波数 | 繰り返しの速さ |
| $\theta$ | 位相差 | 時間的なズレ |
値動きの周期的な部分に注目した時、振幅と角周波数が重要な要素となってきそうです。 これらが分かれば、相場の分析を新たな切り口で行うことができるかもしれません。
振幅
振幅(amplitude)とは、物体が振動しているときの、振動の中心から最大変位までの距離(振動の幅の半分)のことを言います。 つまり、信号の「大きさ・強さ」です。
角周波数
角周波数 ($\omega$)とは回転運動の「速さ」のことを言い、1秒間に何度(ラジアン)進むかを表すので単位は「rad/s」となります。
$$ \omega = 2 \pi f $$
$2 \pi$はラジアンを表し、$f$は周波数を表しています。 式は、1秒間の回転数(周波数)から1秒に何ラジアン進むのか、つまり速さを計算しています。
ラジアン
「角度」を表す際には、「1周を360に分割して、その何個分か」で表現する度数法が使われるのが一般的です。 これは「1周を360としたときの割合」とも言える表現方法です。
この360には数学的な根拠があるわけではなく、1年を360日ぐらいと見積もっていた昔の名残なんだとか。 つまり、1周をいくつと定義するのかは何でも良いのです。
「1周を2$\pi$としたときの割合」としたものがラジアン(radian)です。これは弧度法と呼ばれます。 半径1の円(単位円:unit circle)を想定し、その円周の長さ(2$\pi$)に対し、弧(arc)の長さがどのぐらいの割合を占めるのかで角度を表現します。
周波数
周波数は「1秒間にできる波の数」、回転運動の場合は「1秒間の回転数」を表します。 周波数を表す$f$は「frequency(頻度)」の頭文字で、単位は「Hz(ヘルツ)」を使用します。
周期を$T$とすると、波の周波数$f$は次のように定義されます。
$$ f = \frac{1}{T} $$
複素数
話を先に進めるために、「複素数」に触れておきます。
数は、直線上ではなく平面上に存在すると想定することも可能です。 この概念に従えば、平面上の位置は実数の組として記述できます。 しかし、負の平方根は存在しないため、代数計算には複素数が必要になります。
$$ i = \sqrt{-1}$$
を虚数単位(imaginary number)と定義し、
$$ Z = a + bi $$
の形をとるものをを複素数(complex number)と言います。 また、$a$を実部(real part)、$a$を虚部(imaginary part)と呼びます。
極形式
複素数は、絶対値と偏角を用いた極形式(polar form)で表すこともできます。
$$ Z = r(\cos \theta + i \sin \theta) $$
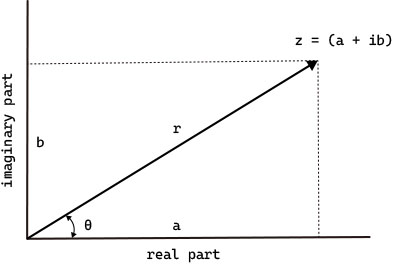
角度が$\theta$のときの極座標上のベクトルの大きさは$r$となります。複素数の直交座標表示と極形式には次のような関係が成り立ちます。
| a | $ r \times \cos (\theta) $ |
| b | $ r \times \sin (\theta) $ |
| r | $ \sqrt{a^2 + b^2}$ |
| $\theta$ | $ \arctan (\frac{b}{a}) $ |
指数形式
複素数は指数関数(exponential function)で表すこともできます。 指数関数は、無限級数展開式の極限値として定義されています。
$$ e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots + \frac{x^n}{n!}$$
三角関数(trigonometric function)も同様に無限級数に展開できます。
$$ \cos (\theta) = 1 - \frac{\theta^2}{2!} + \frac{\theta^4}{4!} - \cdots + (-1)^n \frac{\theta ^{2n}}{(2n)!}$$
$$ \sin (\theta) = \theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} - \cdots + (-1)^{2n-1} \frac{\theta ^{2n-1}}{(2n -1)!}$$
指数関数と三角関数の無限級数展開式で異なるのは、三角関数の展開式ではプラスとマイナスの符号が交互に現れる点です。
しかし、指数関数でも冪指数(power exponent)が虚数になると、三角関数と同じように展開式にプラスとマイナスの符号が交互に現れます。 先ほどの指数関数の展開式において$x = i \theta$と置くと、$e^{i \theta}$の展開式は以下のようになります。
$$ e^{i \theta} = \bigg( 1 - \frac{\theta ^2}{2!} + \frac{\theta ^4}{4!} - \cdots \bigg) + i \bigg( \theta - \frac{\theta ^3}{3!} + \frac{\theta ^5}{5!} - \cdots \bigg)$$
この式の実数部が余弦の展開式、虚数部が正弦の展開式と同じであることから、この式は以下のように書き直すことができます。
$$ e^{i \theta} = \cos (\theta) + i \sin(\theta)$$
同様に、余弦関数と正弦関数を次のように書き直すことも可能です。
$$ e^{i \theta} + e^{-i \theta} = 2 \cos(\theta) $$
$$ e^{i \theta} + e^{-i \theta} = i 2 \sin(\theta) $$
これらの式は複素変数についての重要な公式で、オイラーの公式(Euler’s formula)と呼ばれています。
振幅の測定方法
何度も繰り返されるサイクルは、1サイクル終わるごとに、正弦波が360°、つまり2$\pi$ラジアン進みます。 角周波数とは、周波数に$2 \pi$を掛けたものでした。
$$ \omega = 2 \pi f$$
この定義に従えば、$\omega t$は任意の時間内にサイクルが何ラジアン進むかを表すことになります。 $\omega t$は角度のことなので、$\theta$と$\omega t$は置き換えることが可能です。 このサイクルを複素数の指数形式で表せば以下のようになります。
$$ e^{i \omega t} $$
ベクトルが振幅
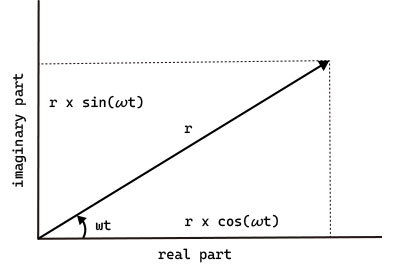
チャートに現れる波形を解析波形と言います。 時間領域における解析波形のサイクルは複素平面状にベクトル($r$)で表すことができます。 $r$は信号の大きさに相当するので、これを振幅と捉えることが可能です。
つまり、解析波形を2つの直交する成分に別けることができれば、そのサイクルの振幅が測定できるということです。 ピタゴラスの定理により、実数部の2乗と虚数部の2乗の合計は、サイクルの振幅の2乗となります。
周期の測定方法

続いて周期を測定する方法です。
最初の測定は時間$t_1$、すなわち位相角$\omega t_1$で行います。次の測定は時間$t_2$、すなわち位相角$\omega t_2$で行います。 このとき、2つの位相角の差は$\Delta \theta$です。 この要領で、位相角の差の合計が2$\pi$(360°)にまで測定を続けます。
$t$を各ローソク足と捉えれば、合計が2$\pi$になるまでに要した本数が周期となります。
ヒルベルト変換
振幅と周期の測定方法が分かりました。 しかし、その前提条件である「解析波形を直交する2つの成分に別けることができれば」が、まだ解決されていません。 この前提条件を満たすために必要になってくるのがヒルベルト変換です。
正弦波状の関数$x(t)$を考えます。
$$ x(t) = A \cos (\omega t) = A \cos (\theta)$$
$x(t)$の値は、振幅$A$ と角周波数 $\omega$ が時不変であれば、時間変数だけで決まり、フーリエスペクトルで求めることができます。
$x(t)$がある時点$t$における価格だとすれば、振幅と角周波数が時不変なんてことはありえません。 振幅と角周波数が時間によって変化する場合は以下のようになります。
$$ x(t) = A (t) \cos (\omega (t) t) = A (t) \cos (\theta (t))$$
$x(t)$が変化したとき、この式では振幅と角周波数のどちらが影響を与えたのかが分かりません。 $t$時点での振幅$A$ = 瞬時振幅 $A(t)$と、$t$時点での角周波数$\theta$ = 瞬時相位 $\theta(t)$を知る必要があります。
しかしながら、$x(t)$の変化だけから、この2つを求めることは不可能です。 両方を同時に求めるためには、時間信号$x(t)$が実信号(1つの値だけを持つ)ではなく、複素信号(2つの値を持つ)であることが必要となります。
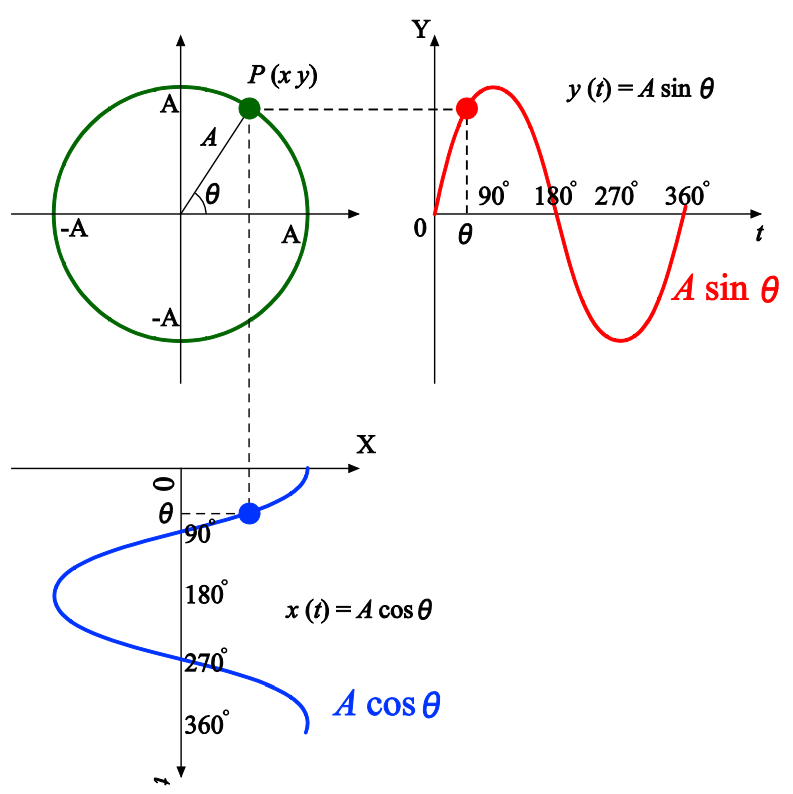
正弦波関数は、複素平面上で回転する点$P(x,y)$の
と見なすことができるので、余弦波から正弦波を作ることができれば、振幅$A$と相位$\theta$を同時に求めることができます。
負の周波数
三角関数には以下の性質があり、$\sin x$が奇関数、$\cos x$が偶関数であることを意味しています(オイラーの贈物:P61)。
$$ \sin(-\omega t) = -\sin(\omega t) $$ $$ \cos(-\omega t) = \cos(\omega t) $$
このことからも分かるように、周波数には「負の周波数」というものが存在し得ます。
チャート上に表れる波形は、複素関数の特殊なケースで、虚数値は持たず、正負いずれかの周波数を持ったものと見なすことが可能です。 ですが、信号をより効率的に処理するためには、一般化した複素関数を使う必要があります。
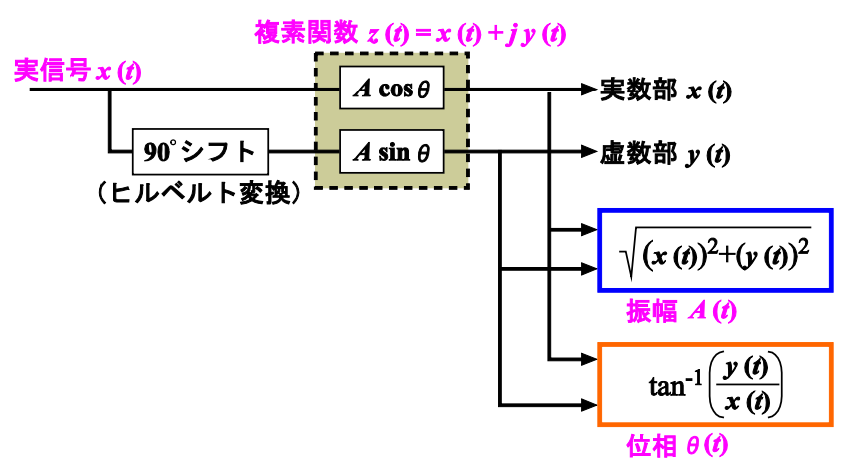
複素関数
点Pを複素関数$z(t)$で表現すると、
$$ z(t) = x(t) + iy(t) = A(t) \cos (\theta (t)) + i A(t) \sin (\theta (t)) $$
$$ z(t) = A (t)e^{i \theta (t)} $$
$$ A(t) = \sqrt{x(t)^2 + y(t)^2} $$
$$ \theta (t) = \tan ^{-1} \Big( \frac{y(t)}{x(t)} \Big) $$
となります。
正弦波関数は、余弦波関数の相位を90度遅延させることで求まります。 したがって、実関数$x(t)$を90度遅延する操作をすることで、複素関数$z(t)$を求めることができます。 時間関数を90度シフトさせる方法の1つがヒルベルト変換です。
このようにして作られる複素信号の
と呼びます。
ヒルベルト変換器
さて、解析信号から複素信号を作成するヒルベルト変換器の実装なのですが、ここからの内容に理解が及んでいません。 とりあえず、メモ書きです。
時間関数を90度シフトさせるヒルベルト変換ですが、具体的には、
という作用をもたらします。
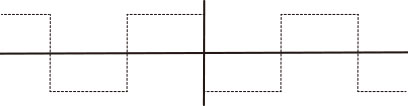
振幅が1のヒルベルト変換器は、角周波数の関数として表すことができます。 これは周期関数なので、グラフに表した指数級数の係数はフーリエ級数によって求めることができます。
指数関数形のフーリエ級数は、
$$ H(z) = \displaystyle\sum_{n=-\infty}^\infty C_n Z^n $$
と書き表すことができます。ここで、$z=e^{i\omega T}$、および$T=1$とおくと、フーリエ変換式は次のようになります。
$$ C_n = \frac{1}{2 \pi} \int_{-\pi}^\pi H(e^{i\omega}) e^{-i n \omega} d \omega$$
$$ H(e^{i\omega}) = \displaystyle\sum_{n=-\infty}^\infty C_n e^{i \omega n}$$
上の式は、デジタルフィルタの係数を求める式です。この中の積分方程式を解くと、次の式が得られます。 ただし、$n \ne 0$とします。
$$ C_n = \frac{2}{\pi} \cdot \frac{\sin ^2 (\frac{\pi n}{2})}{n}$$
$n$の値はフィルタの中心に関係するので、中央の係数は常に0です。 この式における正弦の2乗の項は常に正の値をとり、$n$が奇数の時はその値は1となり、係数は$\frac{1}{n}$となります。
すなわち、フィルタの半分に当たる新しいデータについては係数は正となり、同じくフィルタの残り半分に当たる古いデータの係数は負となります。
ヒルベルト変換器は、係数が負の無限大から正の無限大で拡張されたものが理想となります。 正規化振幅応答を得るために、各係数は全ての係数の和で割るので、ここでは$\frac{\pi}{2}$を無視しても問題ありません。 つまり、周波数成分はフィルタの入力側と出力側とで同じ振幅を持つのが望ましいということです。
近似的な表現
ヒルベルト変換器はある程度の長さで打ち切ることで近似的に表現できます。
フィルタを$n=3$で打ち切り、デトレンド価格を$P$とすると、ヒルベルト変換の直交成分($Q$)は、以下のように書き表すことができます。
$$ Q = 0.25 \times P + 0.75 \times P[2] - 0.75 \times P[4] - 0.25 \times P[6]$$
この短いヒルベルト変換器の遅延はわずか足3本分であるが、フィルタの係数を調整することで振幅応答を改善した方が良い。
$$ Q = 0.0962 \times P + 0.5769 \times P[2] - 0.5769 \times P[4] - 0.0962 \times P[6]$$
この改善したヒルベルト変換器は、使いたい周波数帯の振幅が逓減してしまうという問題を抱える。 改善したヒルベルト変換器は高域通過フィルタとしての機能を持ち、高域通過フィルタは周波数に比例して振幅が減衰するので、周波数が分かれば振幅の減衰を補正することができる。
ヒルベルト変換器の周波数を求めるには、同相成分と直交成分が必要になるの直接には求められない。 しかし、1つ前の足の周波数は分かっている。周波数はゆっくり変化する関数なので、足が1つ違ったくらいでは大きな変化はない。
ヒルベルト変換器が純粋な微分器だとすると、振幅補正項は$\omega$に逆比例する。 周期は周波数の逆数なので、補正項は(周期/2$\pi$)となる。
40本の周期(正規化周波数0.05)では11dBの補正が、20本の周期(正規化周波数0.1)では6.2dBの補正が必要となる。 デシベルを振幅に変換した補正式は以下となる。
$$振幅補正 = (0.075 \times 周期[1] +0.54)$$
位相累積法
最後に、周期を測定する具体的なプロセスについて見ていきます。 そのアプローチはいくつかあり、その1つが「位相累積法」です。
// Smooth the I and Q components before applying the dis criminator.
I1 = .15*T1 + .85*T1[1]
Q1 = .15*Q1 + .85*Q1[1]
// Use Arctangent to compute the current phase.
if abs(T1) > 0 then Phase = ArcTangent(abs(Q1 / T1))
// Resolve the ArcTangent ambiguity for quadrants 2, 3, and 4.
if T1 < 0 and Q1 > 0 then Phase = 180 - Phase
if T1 < 0 and Q1 < 0 then Phase = 180 + Phase
if T1 > 0 and Q1 < 0 then Phase = 180 - Phase
// Compute a differential phase, resolve phase wraparound from quadrant 1 to 4,
// and limit delta phase error.
DeltaPhase = Phase[1] -Phase
if Phase[1] < 90 and Phase > 270 then DeltaPhase = 360 + Phase[1] - Phase
// Limit DeltaPhase to be within the bounds of 6 bar and 50 bar cycles.
if DeltaPhase < 7 then DeltaPhase = 7
if DeltaPhase > 60 then DeltaPhase = 60
// Sum DeltaPhase to seach 360 degree. The sum is the instantaneous period.
InstPeriod = 0
PhaseSum = 0
For count = 0 to 40 begin
PhaseSum = PhaseSum + DeltaPhase[count]
if PhaseSum > 360 and InstPeriod = 0 then
begin
InstPeriod = count
End
End
// Resolve Instantaneous Period error and smooth.
if InstPeriod = 0 then InstPeriod = InstPeriod[1]
Period = .25*InstPeriod + .75*Period[1]

