1標準偏差のショート・ストラングル

2021年10月13日

ショート・ストラングルは、OTMのコールとプットをショートするスプレッドです。相場が大きく動かないことを見込み、タイムディケイの進行とIVの低下から利益を得ようとする戦略です。

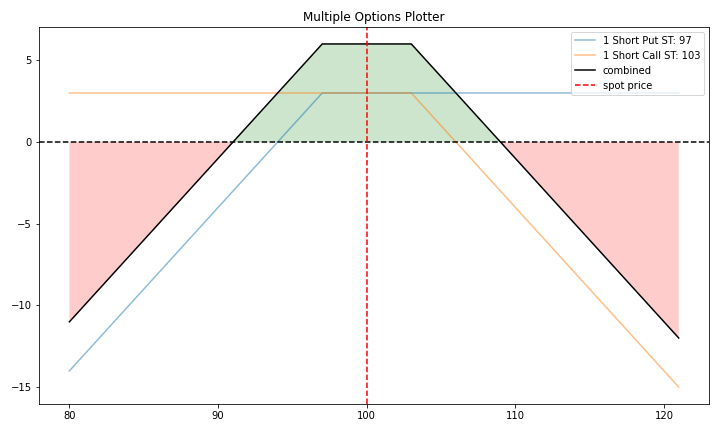
満期を迎えた時、緑の範囲に原資産価格が収まっていると利益となります。最大利益は限定的で、OTMのコールとプットを売った受け取りプレミアムの合計が最大利益です。

浅いOTMを選べば最大利益は増し、深いOTMを選べば最大利益は減少します。浅いOTMを選べば利益を得られる値幅は狭くなり、深いOTMを選べば利益を得られる値幅は広がります。

浅いOTMを選べば、最大利益が増えるが勝率が下がる

深いOTMを選べば、最大利益は減るが勝率が上がる

最大利益と勝率の間にトレードオフの関係があるということです。ショート・ストラングルを建てる上での問題はどの位置のOTMのコールとプットを採用するかに尽きます。

そこで参考になるのが「1標準偏差」です。

IVはオプション価格から逆算されたボラティリティです。別の見方をすれば、IVにより市場参加者が現在想定しているボラティリティが分かることになります。

さて、ボラティリティは年次の変動率のことです。1年後の原資産価格は現在価格の上下IV％の範囲内に68.2%の確率で収まるということを表しています。

突然現れた「68.2%」は正規分布において1標準偏差に収まる確率です。そして、正規分布はBSモデルなどが前提とする「ランダム・ウォーク」が正規分布となるところから来ています。

68.2%の確率でその範囲に収まるというのは面白い考えです。ただ、知りたいのは1年後ではなく、オプションの満期時での範囲になります。

満期時での予想レンジは以下の式で計算できます。

$$ 予想されるレンジ = 原資産価格 \times \frac{IV}{100} \times \sqrt{\frac{残存日数}{365}}$$

以下を条件とすると、

$ 予想されるレンジ = 2000 \times \frac{20}{100} \times \sqrt{\frac{50}{365}}$

$ 予想されるレンジ = 2000 \times 0.2 \times 0.37 = 148 $

1852から2148の範囲に68.2%の確率で収まるだろうということです。

権利行使価格1850のプットと権利行使価格2150のコールをショートすることで、1標準偏差のショート・ストラングルが完成します。

31.8％の確率でコールかプットのどちらかがITMとなりますが、両方がITMになることはありえません。起こりえるのは1850を下回るか、2150を越えるかですから、その確率は半分の15.9％となります。

したがって、このショート・ストラングルで利益を得られる確率は84.1％となります。

（2021年10月13日）内容、計算に自信なし、要検証。